前端面试&笔试爬坑算法 Algorithm

发表于 | 更新于 | 评论数：
17k | 30 分钟

终于来了，算法相关的。 其实个人理解，前端岗位对于算法的要求与其他IT岗位相比，是低得多的。 但是小白我经历了如蚂蚁金服、网易这样的大厂教做人之后，还是觉得，对于一些基本算法、思想的掌握还是必须的。 然后，就把自己遇到的、学到的算法相关的再总结一下，方便自己随时备战面试。

系列笔记：

1.VK的秋招前端奇遇记(一)

2.VK的秋招前端奇遇记(二)

3.VK的秋招前端奇遇记(三)

4.VK的秋招前端奇遇记(四)

5.番外篇：前端面试&笔试算法 Algorithm

排序

JS本身数组的sort方法，可以满足日常业务操作中很多的场景了，所以我认为这也是为什么基本面试会直接让写一个快速排序，因为好像其他排序方法在JS中似乎没什么意义了。

但是在拼多多的面试中，面试官还是让我手写选择排序 冒泡排序 和快速排序 的伪代码。 既然有机会总结，干脆就全部写一遍好了，从基本排序到高级排序来说。

基本排序算法

基本排序的基本思想非常类似，重排列时用的技术基本都是一组嵌套的for循环: 外循环遍历数组的每一项，内循环则用于比较元素。

冒泡排序

最笨最基本最经典点的方法，不管学什么语言，说到排序，第一个接触的就是它了吧。基本思想什么的太经典了，就不复数了，直接用例子说明过程吧：

1
E A D B H

经过一次排列后，变成

1
A E D B H

前两个元素互换了，接下来变成：

1
A D E B H

第二个和第三个互换，继续：

1
A D B E H

第三个和第四个互换，最后，第二个和第三个元素还会互换一次，得到最终的顺序为：

1
A B D E H

好了，其实基本思想就是逐个的比较，下面就实现一下：

1
2
3
4
5
6
7
8
9
10
11
12
13
function bubleSort(arr) {
    var len = arr.length;
    for (let outer = len ; outer >= 2; outer--) {
        for(let inner = 0; inner <=outer - 1; inner++) {
            if(arr[inner] > arr[inner + 1]) {
                let temp = arr[inner];
                arr[inner] = arr[inner + 1];
                arr[inner + 1] = temp;
            }
        }
    }
    return arr;
}

这里有两点需要注意：

  1. 外层循环，从最大值开始递减，因为内层是两两比较，因此最外层当>=2时即可停止；
  2. 内层是两两比较，从0开始，比较inner与inner+1，因此，临界条件是inner<outer -1

在比较交换的时候，就是计算机中最经典的交换策略，用临时变量temp保存值，但是面试官问过我，ES6有没有简单的方法实现？ 有的，如下：

1
2
3
arr2 = [1,2,3,4];
[arr2[0],arr2[1]] = [arr2[1],arr2[0]]  //ES6解构赋值
console.log(arr2)  // [2, 1, 3, 4]

所以，刚才的冒牌排序可以优化如下：

1
2
3
4
5
6
7
8
9
10
11
function bubleSort(arr) {
    var len = arr.length;
    for (let outer = len ; outer >= 2; outer--) {
        for(let inner = 0; inner <=outer - 1; inner++) {
            if(arr[inner] > arr[inner + 1]) {
                [arr[inner],arr[inner+1]] = [arr[inner+1],arr[inner]]
            }
        }
    }
    return arr;
}

选择排序

选择排序是从数组的开头开始，将第一个元素和其他元素作比较，检查完所有的元素后，最小的放在第一个位置，接下来再开始从第二个元素开始，重复以上一直到最后。

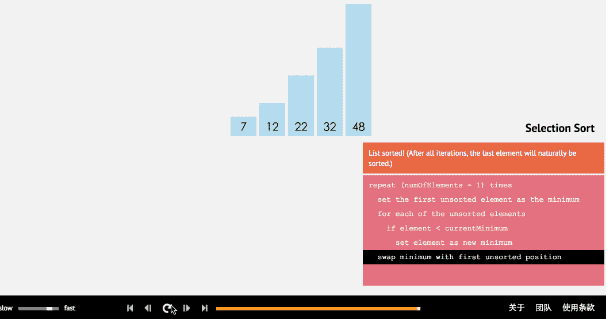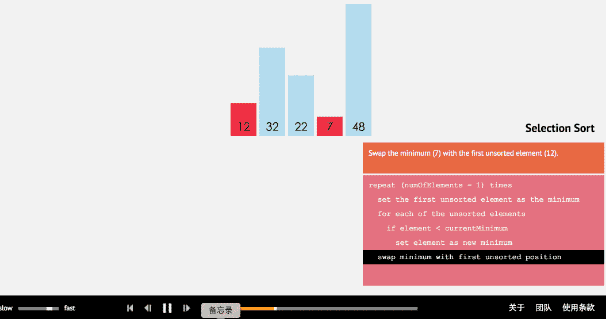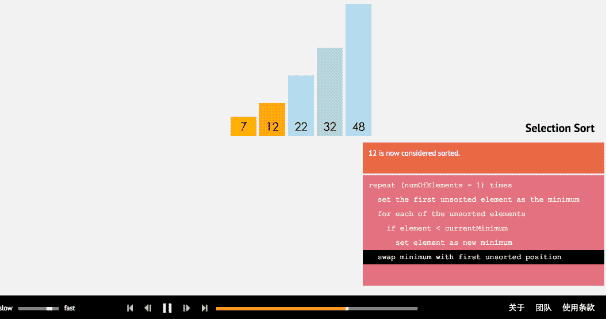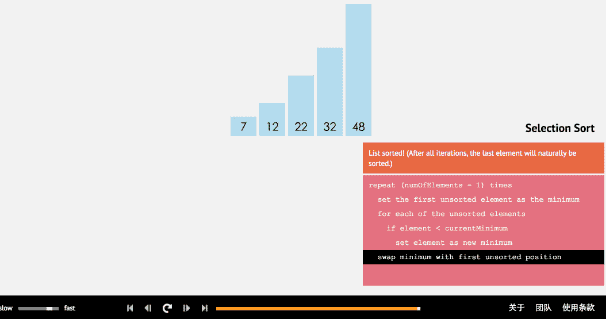
有了刚才的铺垫，我觉得不用再演示了，很简单嘛： 外层循环从0开始到length-1， 然后内层比较，最小的放开头，走你：

1
2
3
4
5
6
7
8
9
10
11
function selectSort(arr) {
    var len = arr.length;
    for(let i = 0 ;i < len - 1; i++) {
        for(let j = i ; j<len; j++) {
            if(arr[j] < arr[i]) {
                [arr[i],arr[j]] = [arr[j],arr[i]];
            }
        }
    }
    return arr
}

简单说两句：

  • 外层循环的i表示第几轮，arr[i]就表示当前轮次最靠前(小)的位置；
  • 内层从i开始，依次往后数，找到比开头小的，互换位置即可

结束，收工！！

插入排序

插入排序核心–扑克牌思想： 就想着自己在打扑克牌，接起来一张，放哪里无所谓，再接起来一张，比第一张小，放左边，继续接，可能是中间数，就插在中间….依次

其实每种算法，主要是理解其原理，至于写代码，都是在原理之上顺理成章的事情：

  • 首先将待排序的第一个记录作为一个有序段
  • 从第二个开始，到最后一个，依次和前面的有序段进行比较，确定插入位置
1
2
3
4
5
6
7
8
9
10
11
12
function insertSort(arr) {
    for(let i = 1; i < arr.length; i++) {  //外循环从1开始，默认arr[0]是有序段
        for(let j = i; j > 0; j--) {  //j = i,将arr[j]依次插入有序段中
            if(arr[j] < arr[j-1]) {
                [arr[j],arr[j-1]] = [arr[j-1],arr[j]];
            } else {
                break;
            }
        }
    }
    return arr;
}

分析： 注意这里两次循环中，i和j的含义：

  1. i是外循环，依次把后面的数插入前面的有序序列中，默认arr[0]为有序的，i就从1开始
  2. j进来后，依次与前面队列的数进行比较，因为前面的序列是有序的，因此只需要循环比较、交换即可
  3. 注意这里的break，因为前面是都是有序的序列，所以如果当前要插入的值arr[j]大于或等于arr[j-1]，则无需继续比较，直接下一次循环就可以了。

时间复杂度

乍一看，好像插入排序速度还不慢，但是要知道： 当序列正好逆序的时候，每次插入都要一次次交换，这个速度和冒泡排序是一样的，时间复杂度O(n²)； 当然运气好，前面是有序的，那时间复杂度就只有O(n)了，直接插入即可。

排序算法 平均时间复杂度 最坏时间复杂度 空间复杂度 是否稳定
冒泡排序 O(n²) O(n²) O(1) 是
选择排序 O(n²) O(n²) O(1) 不是
直接插入排序 O(n²) O(n²) O(1) 是

好了，这张表如何快速记忆呢？ 方法就是一开始写的基本排序算法 。 一开始就说到，基本思想就是两层循环嵌套，第一遍找元素O(n),第二遍找位置O(n)，所以这几种方法，时间复杂度就可以这么简便记忆啦!

高级排序算法

如果所有排序都像上面的基本方法一样，那么对于大量数据的处理，将是灾难性的，老哥，只是让你排个序，你都用了O(n²)。 好吧，所以接下来这些高级排序算法，在大数据上，可以大大的减少复杂度。

快速排序

快速排序可以说是对于前端最最最最重要的排序算法，没有之一了，面试官问到排序算法，快排的概率能有80%以上(我瞎统计的…信不信由你)。

所以快排是什么呢？

快排是处理大数据最快的排序算法之一。它是一种分而治之的算法，通过递归的方式将数据依次分解为包含较小元素和较大元素的不同子序列。该算法不断重复这个步骤直至所有数据都是有序的。

简单说： 找到一个数作为参考，比这个数字大的放在数字左边，比它小的放在右边； 然后分别再对左边和右变的序列做相同的操作:

  1. 选择一个基准元素，将列表分割成两个子序列；
  2. 对列表重新排序，将所有小于基准值的元素放在基准值前面，所有大于基准值的元素放在基准值的后面；
  3. 分别对较小元素的子序列和较大元素的子序列重复步骤1和2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
function quickSort(arr) {
    if(arr.length <= 1) {
        return arr;  //递归出口
    }
    var left = [],
        right = [],
        current = arr.splice(0,1); //注意splice后，数组长度少了一个
    for(let i = 0; i < arr.length; i++) {
        if(arr[i] < current) {
            left.push(arr[i])  //放在左边
        } else {
            right.push(arr[i]) //放在右边
        }
    }
    return quickSort(left).concat(current,quickSort(right)); //递归
}

希尔排序

希尔排序是插入排序的改良算法，但是核心理念与插入算法又不同，它会先比较距离较远的元素，而非相邻的元素。文字太枯燥，还是看下面的动图吧：

在实现之前，先看下刚才插入排序怎么写的：

1
2
3
4
5
6
7
8
9
10
11
12
function insertSort(arr) {
    for(let i = 1; i < arr.length - 1; i++) {  //外循环从1开始，默认arr[0]是有序段
        for(let j = i; j > 0; j--) {  //j = i,将arr[j]依次插入有序段中
            if(arr[j] < arr[j-1]) {
                [arr[j],arr[j-1]] = [arr[j-1],arr[j]];
            } else {
                continue;
            }
        }
    }
    return arr;
}

现在，不同之处是在上面的基础上，让步长按照3、2、1来进行比较，相当于是三层循环和嵌套啦。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
insertSort(arr,[3,2,1]);
function shellSort(arr,gap) {
    console.log(arr)//为了方便观察过程，使用时去除
    for(let i = 0; i<gap.length; i++) {  //最外层循环，一次取不同的步长，步长需要预先给出
        let n = gap[i]; //步长为n
        for(let j = i + n; j < arr.length; j++) { //接下类和插入排序一样，j循环依次取后面的数
            for(let k = j; k > 0; k-=n) { //k循环进行比较，和直接插入的唯一区别是1变为了n
                if(arr[k] < arr[k-n]) {
                    [arr[k],arr[k-n]] = [arr[k-n],arr[k]];
                    console.log(`当前序列为[${arr}] \n 交换了${arr[k]}和${arr[k-n]}`)//为了观察过程
                } else {
                    continue;
                }
            }
        }
    }
    return arr;
}

直接看这个三层循环嵌套的内容，会稍显复杂，这也是为什么先把插入排序写在前面做一个对照。 其实三层循环的内两层完全就是一个插入排序，只不过原来插入排序间隔为1，而希尔排序的间隔是变换的n， 如果把n修改为1，就会发现是完全一样的了。

运行一下看看

1
2
3
var arr = [3, 2, 45, 6, 55, 23, 5, 4, 8, 9, 19, 0];
var gap = [3,2,1];
console.log(shellSort(arr,gap))

结果如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
(12) [3, 2, 45, 6, 55, 23, 5, 4, 8, 9, 19, 0] //初始值
当前序列为[3,2,23,6,55,45,5,4,8,9,19,0] 
 交换了45和23
当前序列为[3,2,23,5,55,45,6,4,8,9,19,0] 
 交换了6和5
当前序列为[3,2,23,5,4,45,6,55,8,9,19,0] 
 交换了55和4
当前序列为[3,2,23,5,4,8,6,55,45,9,19,0] 
 交换了45和8
当前序列为[3,2,8,5,4,23,6,55,45,9,19,0] 
 交换了23和8
当前序列为[3,2,8,5,4,23,6,19,45,9,55,0] 
 交换了55和19
当前序列为[3,2,8,5,4,23,6,19,0,9,55,45] 
 交换了45和0
当前序列为[3,2,8,5,4,0,6,19,23,9,55,45] 
 交换了23和0
当前序列为[3,2,0,5,4,8,6,19,23,9,55,45] 
 交换了8和0
当前序列为[0,2,3,5,4,8,6,19,23,9,55,45] 
 交换了3和0
当前序列为[0,2,3,5,4,8,6,9,23,19,55,45] 
 交换了19和9
当前序列为[0,2,3,4,5,8,6,9,23,19,55,45] 
 交换了5和4
当前序列为[0,2,3,4,5,6,8,9,23,19,55,45] 
 交换了8和6
当前序列为[0,2,3,4,5,6,8,9,19,23,55,45] 
 交换了23和19
当前序列为[0,2,3,4,5,6,8,9,19,23,45,55] 
 交换了55和45

时间复杂度总结

wait？ 不是还有很多排序算法的吗？怎么不继续了？ 是的，其实排序是很深奥的问题，如果研究透各个方法的实现、性能等等，内容恐怕多到爆炸了…而且这个也主要是为前端常见算法 问题的总结，个人觉得到这里就差不多了

排序算法 平均时间复杂度 最坏时间复杂度 空间复杂度 是否稳定
冒泡排序 O(n²) O(n²) O(1) 是
选择排序 O(n²) O(n²) O(1) 不是
直接插入排序 O(n²) O(n²) O(1) 是
快速排序 O(nlogn) O(n²) O(logn) 不是
希尔排序 O(nlogn) O(n^s) O(1) 不是
是否稳定

如果不考虑稳定性，快排似乎是接近完美的一种方法，但可惜它是不稳定的。 那什么是稳定性呢？

通俗的讲有两个相同的数A和B，在排序之前A在B的前面，而经过排序之后，B跑到了A的前面，对于这种情况的发生，我们管他叫做排序的不稳定性，而快速排序在对存在相同数进行排序时就有可能发生这种情况。 

1
2
3
4
5
/*
比如对(5，3A，6，3B ) 进行排序，排序之前相同的数3A与3B，A在B的前面，经过排序之后会变成  
	（3B，3A，5，6）
所以说快速排序是一个不稳定的排序
/*

稳定性有什么意义？ 个人理解对于前端来说，比如我们熟知框架中的虚拟DOM的比较，我们对一个<ul>列表进行渲染，当数据改变后需要比较变化时，不稳定排序或操作将会使本身不需要变化的东西变化，导致重新渲染，带来性能的损耗。

辅助记忆
  • 时间复杂度记忆
    • 冒泡、选择、直接 排序需要两个for循环，每次只关注一个元素，平均时间复杂度为O(n²)(一遍找元素O(n)，一遍找位置O(n)）
    • 快速、归并、希尔、堆基于二分思想，log以2为底，平均时间复杂度为O(nlogn)(一遍找元素O(n)，一遍找位置O(logn))
  • 稳定性记忆-“快希选堆”（快牺牲稳定性）

递归

递归，其实就是自己调用自己。

很多时候我们自己觉得麻烦或者感觉 “想象不过来”，主要是自己和自己较真，因为交给递归，它自己会帮你完成需要做的。

递归步骤：

  • 寻找出口，递归一定有一个出口，锁定出口，保证不会死循环
  • 递归条件，符合递归条件，自己调用自己。

talk is cheap，show me code！

斐波那契数列，每个语言讲递归都会从这个开始，但是既然搞前端，就搞点不一样的吧，从对象的深度克隆(deep clone)说起

Deep Clone ：实现对一个对象(object)的深度克隆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//所谓深度克隆，就是当对象的某个属性值为object或array的时候，要获得一份copy，而不是直接拿到引用值
function deepClone(origin,target) {  //origin是被克隆对象，target是我们获得copy
    var target = target || {}; //定义target
    for(var key in origin) {  //遍历原对象
        if(origin.hasOwnProperty(key)) {
            if(Array.isArray(origin[key])) { //如果是数组
                target[key] = [];
                deepClone(origin[key],target[key]) //递归
            } else if (typeof origin[key] === 'object' && origin[key] !== null) {
                target[key] = {};
                deepClone(origin[key],target[key]) //递归
            } else {
                target[key] = origin[key];
            }
        }
    }
    return target;
}

这个可以说是前端笔试/面试中经常经常遇到的问题了，思路是很清晰的：

  • 出口： 遍历对象结束后return
  • 递归条件： 遇到引用值Array 或 Object

剩下的事情，交给JS自己处理就好了，我们不用考虑内部的层层嵌套，想太多

实战例题

接下来，列举一些自己在最近笔试、面试中遇到的，需要使用递归实现的问题

Q1：Array数组的flat方法实现(2018网易雷火&伏羲前端秋招笔试)

Array的方法flat很多浏览器还未能实现，请写一个flat方法，实现扁平化嵌套数组，如：

1
2
3
4
Array
var arr1 = [1, 2, [3, 4]];
arr1.flat(); 
// [1, 2, 3, 4]

这个问题的实现思路和Deep Clone非常相似，这里实现如下：

1
2
3
4
5
6
7
8
9
10
11
Array.prototype.flat = function() {
    var arr = [];
    this.forEach((item,idx) => {
        if(Array.isArray(item)) {
            arr = arr.concat(item.flat()); //递归去处理数组元素
        } else {
            arr.push(item)   //非数组直接push进去
        }
    })
    return arr;   //递归出口
}

好了，可以测试一下：

1
2
3
arr = [[2],[[2,3],[2]],3,4]
arr.flat()
// [2, 2, 3, 2, 3, 4]

神秘力量的新解法

在评论区的一位小伙伴，提出了更好的办法，很简洁、方便，只用一句话就可以实现需求哦(不过你这样去解答一道网易的“编程题”,不觉得让人家有点难堪嘛~哈哈)

1
2
3
arr.prototype.flat = function() {
    this.toString().split(',').map(item=> +item )
}

好了，惊叹完之后，大概说下实现吧：

  1. toString方法，连接数组并返回一个字符串 '2,2,3,2,3,4'
  2. split方法分割字符串，变成数组['2','2','3','2','3','4']
  3. map方法，将string映射成为number类型2,2,3,2,3,4

Q2 实现简易版的co，自动执行generator

这个问题，详细的解释可以在我之前的文章(从Co剖析和解释generator的异步原理)去看一下，如果对ES6的iterator和generator不太了解的，可以跳过这个问题。

比如实现如下的功能:

1
2
3
4
5
6
7
8
const co = require('co');
co(function *() {
    const url = 'http://jasonplacerholder.typecoder.com/posts/1';
    const response = yield fetch(url);
    const post = yield response.json();
    const title = post.title;
    console.log('Title: ',title);
})

剖析：

  • 第一步找出口，执行器返回的iterator如果状态为done，代表结束，可以出去
  • 递归条件： 取到下一个iterator，进行递归，自我调用
1
2
3
4
5
6
7
8
9
10
11
function run(generat) {
    const iterator = generat();
    function autoRun(iteration) {
        if(iteration.done) {return iteration.value}  //出口
        const anotherPromise = iteration.value;
        anoterPromise.then(x => {
            return autoRun(iterator.next(x))  //递归条件
        })
    }
    return autoRun(iterator.next()) 
}

Q3. 爬楼梯问题

有一楼梯共M级，刚开始时你在第一级，若每次只能跨上一级或二级，要走上第M级，共有多少种走法？

分析： 这个问题要倒过来看，要到达n级楼梯，只有两种方式，从（n-1）级 或 （n-2）级到达的。所以可以用递推的思想去想这题，假设有一个数组s[n], 那么s[1] = 1（由于一开始就在第一级，只有一种方法）， s[2] = 1（只能从s[1]上去 没有其他方法）。

那么就可以推出s[3] ~ s[n]了。

下面继续模拟一下， s[3] = s[1] + s[2]， 因为只能从第一级跨两步， 或者第二级跨一步。

1
2
3
4
5
6
7
function cStairs(n) {
    if(n === 1 || n === 2) {
        return 1;
    } else {
        return cStairs(n-1) + cStairs(n-2)
    }
}

嗯嗯，没错呢，其实就是斐波纳契数列没跑了

Q4.二分查找

二分查找，是在一个有序的序列里查找某一个值，与小时候玩的猜数字游戏非常相啦：

1
2
3
4
5
A: 0 ~ 100 猜一个数字
B: 50
A: 大了
B: 25
A: 对头，就是25

因此，思路也就非常清楚了，这里有递归和非递归两种写法，先说下递归的方法吧：

  • 设定区间,low和high
  • 找出口： 找到target，返回target；
  • 否则寻找，当前次序没有找到，把区间缩小后递归
1
2
3
4
5
6
7
8
9
10
11
12
function binaryFind(arr,target,low = 0,high = arr.length - 1) {
    const n = Math.floor((low+high) /2);
    const cur = arr[n];
    if(cur === target) {
        return `找到了${target},在第${n+1}个`;
    } else if(cur > target) {
        return binaryFind(arr,target,low, n-1);
    } else if (cur < target) {
        return binaryFind(arr,target,n+1,high);
    }
    return -1;
}

接下来，使用循环来做一下二分查找，其实思路基本一致：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
function binaryFind(arr, target) {
    var low = 0,
        high = arr.length - 1,
        mid;
    while (low <= high) {
        mid = Math.floor((low + high) / 2);
        if (target === arr[mid]) {
            return `找到了${target},在第${mid + 1}个`
        }
        if (target > arr[mid]) {
            low = mid + 1;
        } else if (target < arr[mid]) {
            high = mid - 1;
        }
    }
    return -1
}

二叉树和二叉查找树

树的基本概念

这里对基本概念就不详细复习了，在各大资料中有更详尽的介绍，这里就只简单介绍基本概念和术语，然后使用JavaScript实现一个二叉树，并封装其方法。

如图所示，一棵树最上面的几点称为根节点，如果一个节点下面连接多个节点，那么该节点成为父节点，它下面的节点称为子节点，一个节点可以有0个、1个或更多节点，没有子节点的节点叫叶子节点。

二叉树，是一种特殊的树，即子节点最多只有两个，这个限制可以使得写出高效的插入、删除、和查找数据。在二叉树中，子节点分别叫左节点和右节点。

二叉查找树

二叉查找树是一种特殊的二叉树，相对较小的值保存在左节点中，较大的值保存在右节点中，这一特性使得查找的效率很高，对于数值型和非数值型数据，比如字母和字符串，都是如此。现在通过JS实现一个二叉查找树。

节点

二叉树的最小元素是节点，所以先定义一个节点

1
2
3
4
5
6
function Node(data,left,right) {
    this.left = left;
    this.right = right;
    this.data = data;
    this.show = () => {return this.data}
}

这个就是二叉树的最小结构单元

二叉树

1
2
3
function BST() {
    this.root = null //初始化,root为null
}

BST初始化时，只有一个根节点，且没有任何数据。 接下来，我们利用二叉查找树的规则，定义一个插入方法，这个方法的基本思想是:

  1. 如果BST.root === null ，那么就将节点作为根节点
  2. 如果BST.root !==null ，将插入节点进行一个比较，小于根节点，拿到左边的节点，否则拿右边，再次比较、递归。

这里就出现了递归了，因为，总是要把较小的放在靠左的分支。换言之

最左变的叶子节点是最小的数，最右的叶子节点是最大的数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
function insert(data) {
    var node = new Node(data,null,null);
    if(this.root === null) {
        this.root = node
    } else {
        var current = this.root;
        var parent;
        while(true) {
            parent = current;
            if(data < current.data) {
                current = current.left; //到左子树
                if(current === null) {  //如果左子树为空，说明可以将node插入在这里
                    parent.left = node;
                    break;  //跳出while循环
                }
            } else {
                current = current.right;
                if(current === null) {
                    parent.right = node;
                    break;
                }
            }
        }
    }
}

这里，是使用了一个循环方法，不断的去向子树寻找正确的位置。 循环和递归都有一个核心，就是找到出口，这里的出口就是当current 为null的时候，代表没有内容，可以插入。

接下来，将此方法写入BST即可:

1
2
3
4
function BST() {
    this.root = null;
    this.insert = insert;
}

这样子，就可以使用二叉树这个自建的数据结构了:

1
2
3
4
5
6
var bst = new BST()；
bst.insert(10);
bst.insert(8);
bst.insert(2);
bst.insert(7);
bst.insert(5);

但是这个时候，想要看树中的数据，不是那么清晰，所以接下来，就要用到遍历了。

二叉树的遍历

我们知道，树的遍历主要包括

  • 前序遍历 (根左右)
  • 中序遍历 (左根右)
  • 后序遍历 (左右根)

这个只是为了好记忆，我们拿下面的图做一个遍历

前序遍历: 56 22 10 30 81 77 92

中序遍历: 10 22 30 56 77 81 92

后序遍历: 10 30 22 77 92 81 56

这里发现了一些规律：

  1. 前序遍历，因为是根左右，所以最后一个一定是最大的； 第一个一定是root节点；
  2. 中序遍历，在查找二叉树中，一定是从小到大的顺序； 根节点56左边(10/22/30)的一定是左子树的，右边的(77/81/92)一定是右子树的。
  3. 后序遍历，根节点一定在最后
中序遍历的实现

这里就又用到之前的递归了，中序遍历要求: 左！根！右

1
2
3
4
5
6
7
8
9
10
11
12
13
function inOrder(node) {
    if(node !== null) {
        //如果不是null，就一直查找左变，因此递归
        inOrder(node.left);
        //递归结束，打印当前值
        console.log(node.show());
        //上一次递归已经把左边搞完了，右边
        inOrder(node.right);
    }
}

//在刚才已有bst的基础上执行命令
inOrder(bst.root);

通过递归，实现了中序遍历，上面打印出的结果如下:

1
2
3
4
5
2
5
7
8
10
前序遍历&后序遍历

如果刚才的递归过程搞清楚，那这个就再简单不过了

1
2
3
4
5
6
7
8
function preOrder(node) {
    if(node !== null) {
        //根左右
        console.log(node.show());
        preOrder(node.left);
        preOrder(node.right);
    }
}

ok,趁热打铁，就把后序遍历的方法也一并写入，如下:

1
2
3
4
5
6
7
8
function postOrder(node) {
    if(node !== null) {
        //左右根
        postOrder(node.left);
        postOrder(node.right);
        console.log(node.show())
    }
}

好了，可以去尝试两种方法打印出来的结果了:

1
2
preOrder(bst.root);
postOrder(bst.root);

二叉树的查找

在二叉树这种数据结构中进行数据查找是最方便的，现在我们就对查找最小值、最大值和特定值进行一个梳理：

  • 最小值： 最左子树的叶子节点
  • 最大值： 最右子树的叶子节点
  • 特定值： target与current进行比较，如果比current大，在current.right进行查找，反之类似。

清楚思路后，就动手来写：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//最小值
function getMin(bst) {
    var current = bst.root;
    while(current.left !== null) {
        current = current.left;
    }
    return current.data;
}

//最大值
function getMax(bst) {
    var current = bst.root;
    while(current.right !== null) {
        current = current.right;
    }
    return current.data;
}

最大、最小值都是非常简单的，下面主要看下如何通过

1
2
3
4
5
6
7
8
9
10
11
12
13
14
function find(target,bst) {
    var current = bst.root;
    while(current !== null) {
        if(target === current.data) {
            return true;
        }
        else if(target > current.data) {
            current = current.right;
        } else if(target < current.data) {
            current = current.left;
        }
    }
    return -1;
}

其实核心，仍然是通过一个循环和判断，来不断的向下去寻找，这里的思想其实和二分查找是有点类似的。

哇…

没想到今天去整理排序 花了这么久…嗯..然而这篇文章已经够长了

接下来我会把之前笔试遇到的题目和一些常用的算法问题，一一记录，前端很多算法都是和数组、字符串处理息息相关的，所以对正则表达式、数组常用方法的掌握也很重要，简单总结下知识点：

  • 正则表达式
    • 字符串相关方法
    • str.split()
    • str.replace()
    • str.match()
    • reg.test()
    • reg.exec()
  • 数组方法
    • Array.map() 映射，有返回值，不改变数组本身
    • Array.forEach() 遍历，无返回值
    • Array.filter() 过滤，返回true时返回,false时不返回
    • Array.splice/slice/join等
    • for…of 遍历,iterator相关知识点

未完待续….

内容会持续更新，最快的当然还是在github上，然后会同步到掘金，github传送门

参考资料

  1. 排序算法时间复杂度、空间复杂度、稳定性比较
  2. 算法学习记录–希尔排序
  3. 快速排序简单理解
  4. 数据结构与算法Javascript描述
0%